(本小题满分12分)
为了解我区中学生的体质状况及城乡大学生的体质差异,对银川地区部分大学的学生进行了身高、体重和肺活量的抽样调查。现随机抽取100名学生,测得其身高情况如下表所示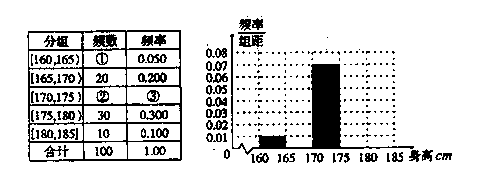
(1)请在频率分布表中的①、②、③位置填上相应的数据,并补全频率分布直方图,再根据频率分布直方图估计众数的值;
(2)若按身高分层抽样,抽取20人参加2011年庆元旦“步步高杯”全民健身运动其中有3名学生参加越野比赛,记这3名学生中“身高低于170Ccm”的人数为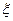 ,求
,求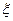 的分布列及期望。
的分布列及期望。
相关知识点
推荐套卷
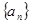 中,
中,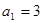 ,前n项和为
,前n项和为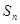
 ,当
,当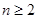 时,有
时,有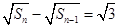 .(1)求数列
.(1)求数列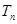 是数列
是数列 的前
的前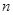 项和,若
项和,若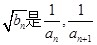 的等比中项,求
的等比中项,求 中,
中,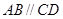 ,
,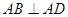 ,且
,且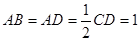 .
.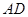 为一边向梯形外作正方形
为一边向梯形外作正方形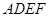 ,然后沿边
,然后沿边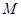 为
为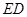 的中点,如图2.
的中点,如图2.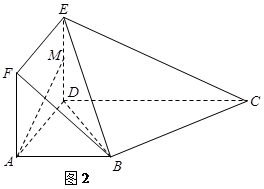
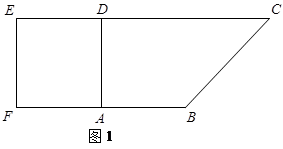
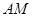 ∥平面
∥平面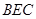 ;
; ;
; 到平面
到平面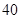 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在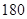 分钟到
分钟到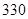 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计,得到如下频率分布表:
个组统计,得到如下频率分布表: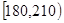
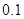

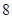
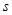
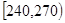
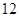
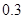
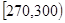

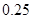
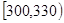
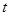
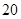 名进行研究,问应抽取多少名第一组的学生?
名进行研究,问应抽取多少名第一组的学生?
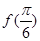 的值;
的值;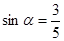 ,且
,且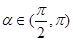 ,求
,求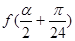 .
.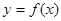 的定义域为
的定义域为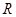 ,若存在常数
,若存在常数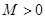 ,使得
,使得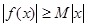 对一切实数
对一切实数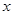 均成立,则称
均成立,则称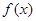 为“圆锥托底型”函数.
为“圆锥托底型”函数.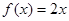 ,
,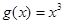 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.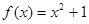 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出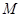 的最大值.
的最大值.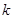 、
、 满足什么条件,
满足什么条件,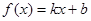 是“圆锥托底型” 函数.
是“圆锥托底型” 函数. 粤公网安备 44130202000953号
粤公网安备 44130202000953号