（本小题满分14分）
某单位为解决职工的住房问题，计划征用一块土地盖一幢总建筑面积为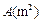
的宿舍楼．已知土地的征用费为2388元/
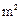，且每层的建筑面积相同，土地的征用面积为第一层的2．5倍．经工程技术人员核算，第一．二层的建筑费用都为445元/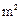，以后每增高一层，其建筑费用就增加30元/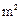．试设
计这幢宿舍楼的楼高层数，使总费用最小，并求出其最小费用．（总费用为建筑费用和征地费用之和）
），则
的值为 。
＋
＋
＋
的值域是 。
（a
＋a＋1），q＝log
＋a＋1），则p、q的大小关系是 。
有最大值2，求实数
的取值.
的图象经过点（-1，3），且f（x）在（-1，+∞）上恒有f（x）＜3，求函数f（x）.推荐套卷
（本小题满分14分）
某单位为解决职工的住房问题，计划征用一块土地盖一幢总建筑面积为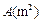的宿舍楼．已知土地的征用费为2388元/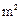，且每层的建筑面积相同，土地的征用面积为第一层的2．5倍．经工程技术人员核算，第一．二层的建筑费用都为445元/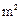，以后每增高一层，其建筑费用就增加30元/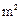．试设计这幢宿舍楼的楼高层数，使总费用最小，并求出其最小费用．（总费用为建筑费用和征地费用之和）
粤公网安备 44130202000953号