(本小题满分14分)已知长方形 ,
,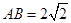 ,
,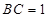 ,以
,以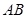 的中点
的中点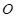 为
为
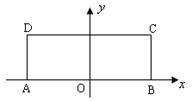
原点建立如图所示的平面直角坐标系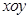 .
.
(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(2)设椭圆上任意一点为P,在x轴上有一个动点Q(t,0),其中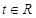 ,探究
,探究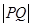 的最
的最
小值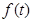 。
。
推荐套卷
(本小题满分14分)已知长方形 ,
,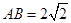 ,
,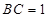 ,以
,以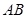 的中点
的中点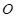 为
为
原点建立如图所示的平面直角坐标系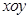 .
.
(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(2)设椭圆上任意一点为P,在x轴上有一个动点Q(t,0),其中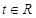 ,探究
,探究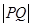 的最
的最
小值 。
。