（本小题满分12分）某地决定新建A，B，C三类工程，A，B，C三类工程所含项目的个数分别占总项目数的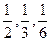
（总项目数足够多），现有3名工人独立地从中任选一个项目参与建设
（Ⅰ）求他们选择的项目所属工程
类别相同的概率；
（Ⅱ）记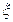
为3人中选择的项目属于B类工程或C类工程的人数，求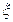的分布列及数学期望.
相关试题
在
上为增函数，在[0,2]上为减函数，
。
的值；
。
满足
,
=
。
；
的解析式，并用数学归纳法证明。
展开式中常数项为1120，其中实数
为常数。
的三个内角，向量
，且
。
（1）求
的值；
分别是角A，B，C的对边，且
。
的值；
，求三角形ABC的面积。推荐套卷
（本小题满分12分）某地决定新建A，B，C三类工程，A，B，C三类工程所含项目的个数分别占总项目数的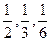（总项目数足够多），现有3名工人独立地从中任选一个项目参与建设
（Ⅰ）求他们选择的项目所属工程类别相同的概率；
（Ⅱ）记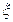为3人中选择的项目属于B类工程或C类工程的人数，求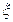的分布列及数学期望.
粤公网安备 44130202000953号