已知函数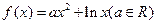 .
.
(1)当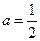 时,求
时,求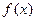 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;
(2)如果函数 ,
,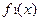 ,
,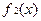 ,在公共定义域D上,满足
,在公共定义域D上,满足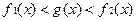 ,那么就称为
,那么就称为 为
为 的“活动函数”.
的“活动函数”.
已知函数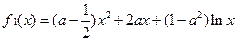 ,
,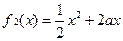 .
.
①若在区间 上,函数
上,函数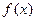 是
是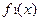 ,
,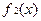 的“活动函数”,求
的“活动函数”,求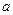 的取值范围;
的取值范围;
②当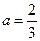 时,求证:在区间
时,求证:在区间 上,函数
上,函数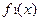 ,
,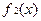 的“活动函数”有无穷多个.
的“活动函数”有无穷多个.
推荐套卷
已知函数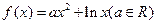 .
.
(1)当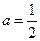 时,求
时,求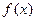 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;
(2)如果函数 ,
,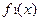 ,
,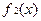 ,在公共定义域D上,满足
,在公共定义域D上,满足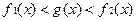 ,那么就称为
,那么就称为 为
为 的“活动函数”.
的“活动函数”.
已知函数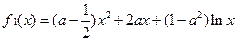 ,
,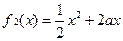 .
.
①若在区间 上,函数
上,函数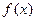 是
是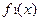 ,
,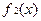 的“活动函数”,求
的“活动函数”,求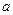 的取值范围;
的取值范围;
②当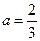 时,求证:在区间
时,求证:在区间 上,函数
上,函数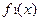 ,
,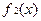 的“活动函数”有无穷多个.
的“活动函数”有无穷多个.