（、（本题16分）
如图，有一块抛物线形状的钢板，计划将此钢板切割成等腰梯形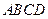
的形状，使得
都落在抛物线上，点
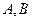关于抛物线的轴对称，且
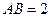，抛物线的顶点到底边的距离是
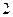，记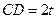
，梯形面积为
．
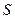（1）以抛物线的顶点为坐标原点，其对称轴为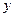
轴建立坐标系，使抛物线开口向下，求出该抛物线的方程；
（2）求面积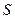关于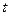
的函数解析式，并写出其定义域；
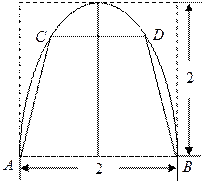（3）求面积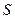的最大值．
相关试题
为何值时，方程
有一个解？有两个解？有三个解？
;
.
，
； 
=
，满足
，求实数
的取值范围.
的首项
。
是等比数列，并求
是偶函数，且对任意
均有
，当
时，
，求使
恒成立的
的取值范围。
其前
项和
，满足
，且
。
的值；
；相关知识点
推荐套卷
（、（本题16分）
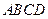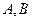如图，有一块抛物线形状的钢板，计划将此钢板切割成等腰梯形的形状，使得都落在抛物线上，点关于抛物线的轴对称，且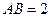，抛物线的顶点到底边的距离是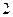，记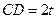，梯形面积为．
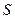（1）以抛物线的顶点为坐标原点，其对称轴为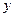轴建立坐标系，使抛物线开口向下，求出该抛物线的方程；
（2）求面积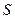关于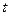的函数解析式，并写出其定义域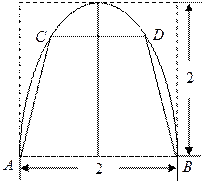；（3）求面积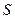的最大值．
粤公网安备 44130202000953号