20.（本小题满分8分）如图，AB是⊙O的直径，PA⊥⊙O所在的平面，C是圆上一点，∠ABC = 30°，PA = AB.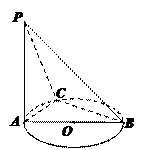 
(1)求证：平面PAC⊥平面PBC；
(2)求直线PC与平面ABC所成角的正切值；
(3)求二面角A—PB—C的正弦值.
，求下列各式的值．
＋
；
；
.
，2tanα＋3sinβ＝7，且tanα－6sinβ＝1，求sinα的值．
－
.推荐套卷
20.（本小题满分8分）如图，AB是⊙O的直径，PA⊥⊙O所在的平面，C是圆上一点，∠ABC = 30°，PA = AB. 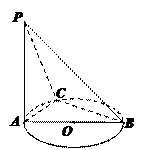(1)求证：平面PAC⊥平面PBC；
(2)求直线PC与平面ABC所成角的正切值；
(3)求二面角A—PB—C的正弦值.
粤公网安备 44130202000953号