如图，在五面体ABCDEF中，FA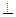
平面ABCD，AD//BC//FE，AB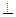AD，AF＝AB＝BC＝FE＝
AD.
（Ⅰ）求异面直线BF与DE所成角的余弦值；
（Ⅱ）在线段CE上是否存在点M，使得直线AM与平面CDE所成角的正弦值为
？若存在，试确定
点M的位置；若不存在，请说明理由.
推荐套卷
如图，在五面体ABCDEF中，FA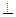平面ABCD，AD//BC//FE，AB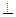AD，AF＝AB＝BC＝FE＝AD.
（Ⅰ）求异面直线BF与DE所成角的余弦值；
（Ⅱ）在线段CE上是否存在点M，使得直线AM与平面CDE所成角的正弦值为？若存在，试确定点M的位置；若不存在，请说明理由.
粤公网安备 44130202000953号