（本小题满分12分）
某公司近年来科研费用支出
万元与公司所获得利润
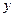万元之间有如下的统计数据：
|
2 |
3 |
4 |
5 |
|
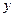18 |
27 |
32 |
35 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出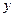关于的线性回归方程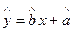
；
(3)试根据(2)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式: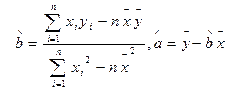
相关试题
某研究性学习小组有
名同学．
（1）这名同学排成一排照相，则同学甲与同学乙相邻的排法有多少种？
（2）从名同学中选
人参加班级
接力比赛，则同学丙不跑第一棒的安排方法有多少种？
，
．
的最小正周期和单调增区间；
上的最小值和最大值；
，求使
的
取值范围．
＋sin
的值；
的值．
，求
的值。相关知识点
推荐套卷
粤公网安备 44130202000953号