(本小题满分14分)
已知椭圆方程为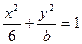 (
(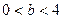 ),抛物线方程为
),抛物线方程为 .过抛物线的焦点作
.过抛物线的焦点作 轴的垂线,与抛物线在第一象限的交点为
轴的垂线,与抛物线在第一象限的交点为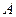 ,抛物线在点
,抛物线在点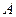 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点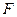 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设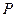 为椭圆上的动点,由
为椭圆上的动点,由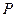 向
向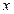 轴作垂线
轴作垂线 ,垂足为
,垂足为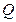 ,且直线
,且直线 上一点
上一点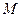 满足
满足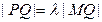 ,求点
,求点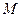 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
推荐套卷
(本小题满分14分)
已知椭圆方程为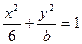 (
(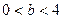 ),抛物线方程为
),抛物线方程为 .过抛物线的焦点作
.过抛物线的焦点作 轴的垂线,与抛物线在第一象限的交点为
轴的垂线,与抛物线在第一象限的交点为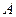 ,抛物线在点
,抛物线在点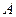 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点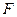 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设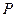 为椭圆上的动点,由
为椭圆上的动点,由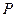 向
向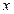 轴作垂线
轴作垂线 ,垂足为
,垂足为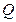 ,且直线
,且直线 上一点
上一点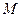 满足
满足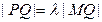 ,求点
,求点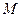 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.