(本小题满分13分)
已知等差数列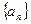 的公差为
的公差为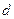 ,前
,前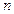 项和为
项和为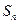 ,且满足
,且满足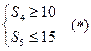 ,
,
(1)试用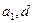 表示不等式组
表示不等式组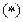 ,并在给定的坐标系中用阴影画出不等式组表示的平面区域;
,并在给定的坐标系中用阴影画出不等式组表示的平面区域;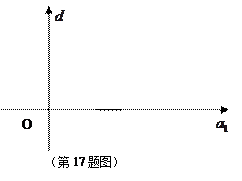 (2)求
(2)求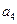 的最大值,并指出此时数列
的最大值,并指出此时数列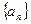 的公差
的公差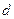 的值.
的值.
相关知识点
推荐套卷
(本小题满分13分)
已知等差数列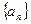 的公差为
的公差为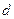 ,前
,前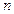 项和为
项和为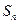 ,且满足
,且满足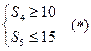 ,
,
(1)试用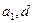 表示不等式组
表示不等式组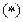 ,并在给定的坐标系中用阴影画出不等式组表示的平面区域;
,并在给定的坐标系中用阴影画出不等式组表示的平面区域;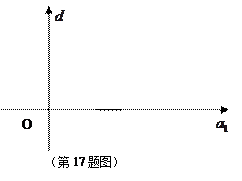 (2)求
(2)求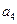 的最大值,并指出此时数列
的最大值,并指出此时数列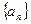 的公差
的公差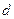 的值.
的值.