(本小题满分12分)
已知数列 满足
满足
(Ⅰ)欲求 的通项公式,若能找到一个函数
的通项公式,若能找到一个函数

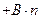
 (A、B、C未必常数),把递推
(A、B、C未必常数),把递推 关系变成
关系变成
 后,就容易求出
后,就容易求出 的通项了.请问:这样的
的通项了.请问:这样的 存在吗?
存在吗? 的通项公式是什么?
的通项公式是什么?
(Ⅱ)记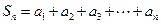 ,若不等式
,若不等式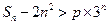 对任意
对任意 都成立,求实数
都成立,求实数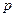 的
的 取值范围。
取值范围。
推荐套卷
(本小题满分12分)
已知数列 满足
满足
(Ⅰ)欲求 的通项公式,若能找到一个函数
的通项公式,若能找到一个函数

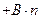
 (A、B、C未必常数),把递推
(A、B、C未必常数),把递推 关系变成
关系变成
 后,就容易求出
后,就容易求出 的通项了.请问:这样的
的通项了.请问:这样的 存在吗?
存在吗? 的通项公式是什么?
的通项公式是什么?
(Ⅱ)记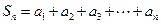 ,若不等式
,若不等式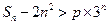 对任意
对任意 都成立,求实数
都成立,求实数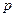 的
的 取值范围。
取值范围。