(本小题满分12分)如图,已知圆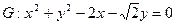 经过椭圆
经过椭圆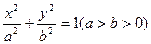 的右焦点F及上顶点B.过点
的右焦点F及上顶点B.过点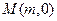 作倾斜角为
作倾斜角为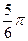 的直线
的直线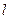 交椭圆于C、D两点.
交椭圆于C、D两点.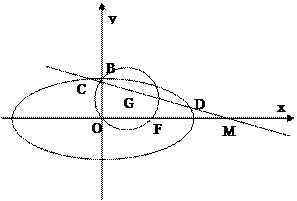
(1)求椭圆的方程;
(2)若点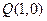 恰在以线段CD为直径
恰在以线段CD为直径
的圆的内 部,求实数
部,求实数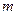 范围.
范围.
相关知识点
推荐套卷
(本小题满分12分)如图,已知圆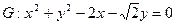 经过椭圆
经过椭圆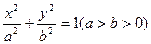 的右焦点F及上顶点B.过点
的右焦点F及上顶点B.过点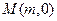 作倾斜角为
作倾斜角为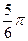 的直线
的直线 交椭圆于C、D两点.
交椭圆于C、D两点.
(1)求椭圆的方程;
(2)若点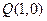 恰在以线段CD为直径
恰在以线段CD为直径
的圆的内 部,求实数
部,求实数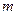 范围.
范围.