（1）将一批重490吨的货物分配给甲、乙两船运输．现甲、乙两船已分别运走其任务数的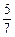
、
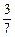，在已运走的货物中，甲船比乙船多运30吨．求分配给甲、乙两船的任务数各多少吨？
（2）自编一道应用题，要求如下：
①是路程应用题．三个数据100，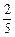
，
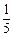必须全部用到，不添加其他数据．
②只要编题，不必解答．
年的用电情况如下图1：
结CD，若AD＝2，BD＝4，
相关知识点
推荐套卷
（1）将一批重490吨的货物分配给甲、乙两船运输．现甲、乙两船已分别运走其任务数的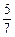、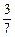，在已运走的货物中，甲船比乙船多运30吨．求分配给甲、乙两船的任务数各多少吨？
（2）自编一道应用题，要求如下：
①是路程应用题．三个数据100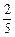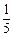，，必须全部用到，不添加其他数据．
②只要编题，不必解答．
粤公网安备 44130202000953号