设 ,
, , 其中
, 其中 是不等于零的常数,
是不等于零的常数,
(1)、(理)写出 的定义域;
的定义域;
(文) 时,直接写出
时,直接写出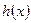 的值域
的值域
(2)、(文、理)求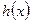 的单调递增区间(理5分,文8分);
的单调递增区间(理5分,文8分);
(3)、已知函数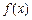
 ,定义:
,定义: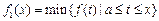
 ,
,
 .其中,
.其中, 表示函数
表示函数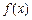 在
在 上的最小值,
上的最小值,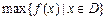 表示函数
表示函数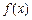 在
在
 上的最大值.例如:
上的最大值.例如: ,
, ,则
,则 ,
, ,
,
(理)当 时,设
时,设 ,不等式
,不等式
恒成立,求 的取值范围;
的取值范围;
(文)当 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围;
相关知识点
推荐套卷
设 ,
, , 其中
, 其中 是不等于零的常数,
是不等于零的常数,
(1)、(理)写出 的定义域;
的定义域;
(文) 时,直接写出
时,直接写出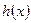 的值域
的值域
(2)、(文、理)求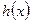 的单调递增区间(理5分,文8分);
的单调递增区间(理5分,文8分);
(3)、已知函数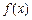
 ,定义:
,定义: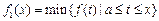
 ,
,
 .其中,
.其中, 表示函数
表示函数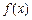 在
在 上的最小值,
上的最小值,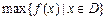 表示函数
表示函数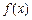 在
在
 上的最大值.例如:
上的最大值.例如: ,
, ,则
,则 ,
, ,
,
(理)当 时,设
时,设 ,不等式
,不等式
恒成立,求 的取值范围;
的取值范围;
(文)当 时,
时, 恒成立,求
恒成立,求 的取值范围;
的取值范围;