本题满分14分)
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如下表1、表2.
表1:男 生身高频数分布表
生身高频数分布表
表2:女生身高频数分布表
(1)求该校男生的人数并完成下面频率分布直方图;
(2)估计该校学生身高(单位:cm)在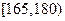 的概率;
的概率;
(3)在男生样本中,从身高(单位:cm)在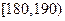 的男生中任选3人,设
的男生中任选3人,设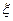 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在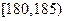 的人数,求
的人数,求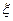 的分布列和数学期望.
的分布列和数学期望.
相关知识点
推荐套卷
 .
. 及
及 ;
;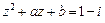 ,求实数
,求实数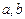 的值.
的值.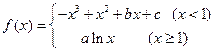 的图象过点
的图象过点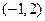 ,且在点
,且在点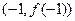 处的切线与直线
处的切线与直线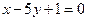 垂直.
垂直. 的值;(6分)
的值;(6分)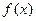 在
在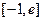 (
(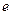 为自然对数的底数)上的最大值;(5分)
为自然对数的底数)上的最大值;(5分)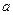 ,曲线
,曲线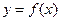 上是否存在两点
上是否存在两点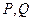 ,使得
,使得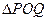 是以
是以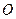 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在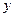 轴上?(5分)
轴上?(5分) 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
 (rad),将
(rad),将 表示成
表示成 的函数;并写出函数的定义域. (5分)
的函数;并写出函数的定义域. (5分) (km),将
(km),将 的函数;并写出函数的定义域.(5分)
的函数;并写出函数的定义域.(5分) (2)
(2) +
+ ≥8; (3)
≥8; (3)  +
+  ≥
≥ . (5分+5分+5分)
. (5分+5分+5分) 粤公网安备 44130202000953号
粤公网安备 44130202000953号