(本题满分15分)
已知偶函数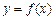 满足:当
满足:当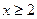 时,
时,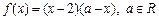 ,当
,当 时,
时,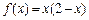
(1) 求当 时,
时, 的表达式;
的表达式;
(2) 若直线 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。
(3) 试讨论当实数 满足什么条件时,函数
满足什么条件时,函数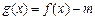 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。
推荐套卷
(本题满分15分)
已知偶函数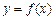 满足:当
满足:当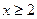 时,
时,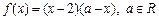 ,当
,当 时,
时,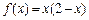
(1) 求当 时,
时, 的表达式;
的表达式;
(2) 若直线 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。
(3) 试讨论当实数 满足什么条件时,函数
满足什么条件时,函数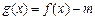 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。