（本小题满分12分）如图所示，已知A、B、C是椭圆
上三点，其中点A的坐标为
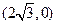，BC过椭圆的中心O，且
（Ⅰ）求点C的坐标及椭圆E的方程；
（Ⅱ）若椭圆E上存在两点P，Q，使得
的平分线总垂直于z轴，试判断向量
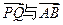是否共线，并给出证明．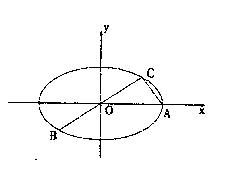
相关试题
是坐标平面内的任意两个角，且
，请写出两角差的余弦公式并加以证明.
的前
项和为
，
，
，等差数列
满足
，
．
，不等式
恒成立，求实数
的取值范围．
满足
，
，数列
满足
．
，求满足不等式
的所有正整数
的值．
，
，且
∥
，其中
是
的内角．
，求
的最大值．
是等差数列，数列
是各项都为正数的等比数列，且 
， 
，
．
的前n项和
．推荐套卷
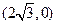（本小题满分12分）如图所示，已知A、B、C是椭圆上三点，其中点A的坐标为，BC过椭圆的中心O，且
（Ⅰ）求点C的坐标及椭圆E的方程；
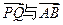（Ⅱ）若椭圆E上存在两点P，Q，使得的平分线总垂直于z轴，试判断向量是否共线，并给出证明．
粤公网安备 44130202000953号