如图,在六面体
中,四边形
是边长为2的正方形,四边形
是边长为1的正方形,
,
,
.
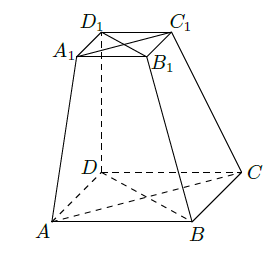
(Ⅰ)求证:
共面,
共面;
(Ⅱ)求证:
;
(Ⅲ)求二面角
的大小(用反三角函数值表示).
推荐套卷
如图,在六面体
中,四边形
是边长为2的正方形,四边形
是边长为1的正方形,
,
,
.

(Ⅰ)求证:
共面,
共面;
(Ⅱ)求证:
;
(Ⅲ)求二面角
的大小(用反三角函数值表示).