某工厂每月生产某种产品三件,经检测发现,工厂生产该产品的合格率为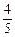 ,已知生产一件合格品能盈利25万元,生产一件次品将会亏损10万元,假设该产品任何两件之间合
,已知生产一件合格品能盈利25万元,生产一件次品将会亏损10万元,假设该产品任何两件之间合 格与否相互没有影响.
格与否相互没有影响.
(Ⅰ)求工厂每月盈利额ξ(万元)的所有可能取值;
(Ⅱ)若该工厂制定了每月盈利额不低于40万元的目标,求该工厂达到盈利目标的概率;
(Ⅲ)求工厂每月盈利额ξ的分布列和数学期望.
相关知识点
推荐套卷
某工厂每月生产某种产品三件,经检测发现,工厂生产该产品的合格率为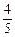 ,已知生产一件合格品能盈利25万元,生产一件次品将会亏损10万元,假设该产品任何两件之间合
,已知生产一件合格品能盈利25万元,生产一件次品将会亏损10万元,假设该产品任何两件之间合 格与否相互没有影响.
格与否相互没有影响.
(Ⅰ)求工厂每月盈利额ξ(万元)的所有可能取值;
(Ⅱ)若该工厂制定了每月盈利额不低于40万元的目标,求该工厂达到盈利目标的概率;
(Ⅲ)求工厂每月盈利额ξ的分布列和数学期望.