已知双曲线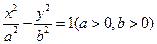
，顺次连接其实轴、虚轴端点所得四边形的面积为8，
（1）求双曲线焦距的最小值，并求出焦距最小时的双曲线方程；
（2）设A、B是双曲线上关于中心对称的两点，P是双曲线上另外一点，若直线PA、PB的斜率乘积等于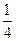
，求双曲线方程。
相关试题
，其中
，若
，且图象的一条对称轴离一个对称中心的最近距离是
．
的解析式；
是
的三个内角，且
，求
的取值范围
的图像上每一点的横坐标伸长到原来的2倍，纵坐标不变，然后再向左平移
个单位后得到一个最小正周期为2
的奇函数
.
的值；
的单调区间和最值．
，求：
；
的最小值是
，求实数
的值．
，求
的值.
.
中，
∥
，试求
与
满足的关系．
，求相关知识点
推荐套卷
已知双曲线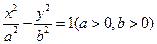，顺次连接其实轴、虚轴端点所得四边形的面积为8，
（1）求双曲线焦距的最小值，并求出焦距最小时的双曲线方程；
（2）设A、B是双曲线上关于中心对称的两点，P是双曲线上另外一点，若直线PA、PB的斜率乘积等于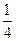，求双曲线方程。
粤公网安备 44130202000953号