已知等比数列{an}满足a1+a6=11，且a3a4=
.
（1）求数列{an}的通项an；
（2）如果至少存在一个自然数m，恰使
，
，am+1+
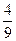这三个数依次成等差数列，问这样的等比数列{an}是否存在?若存在，求出通项公式；若不存在，请说明理由.
相关试题
所表示的平面区域为
，记
.
、
、
的值及
的表达式；
，
为
的前
项和，求
,cosB=
, 试判断三角形的形状．推荐套卷
已知等比数列{an}满足a1+a6=11，且a3a4=.
（1）求数列{an}的通项an；
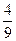（2）如果至少存在一个自然数m，恰使，，am+1+这三个数依次成等差数列，问这样的等比数列{an}是否存在?若存在，求出通项公式；若不存在，请说明理由.
粤公网安备 44130202000953号