(本小题满分12分)


已知在3支不同编号的枪中有2支已经试射校正过,1支未经试射校正。某射手若使用其中校正过的枪,每射击一次击中目标的概率为 ;若使用其中未校正的枪,每射击一次击中目标的概率为
;若使用其中未校正的枪,每射击一次击中目标的概率为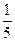 ,假定每次射击是否击中目标相互之间没有影响。
,假定每次射击是否击中目标相互之间没有影响。
(I)若该射手用这2支已经试射校正过的枪各射击一次,求目标被击中的次数为偶数的概率;
(II)若该射手用这3支抢各射击一次,求目标至多被击中一次的概率。
推荐套卷
(本小题满分12分)


已知在3支不同编号的枪中有2支已经试射校正过,1支未经试射校正。某射手若使用其中校正过的枪,每射击一次击中目标的概率为 ;若使用其中未校正的枪,每射击一次击中目标的概率为
;若使用其中未校正的枪,每射击一次击中目标的概率为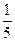 ,假定每次射击是否击中目标相互之间没有影响。
,假定每次射击是否击中目标相互之间没有影响。
(I)若该射手用这2支已经试射校正过的枪各射击一次,求目标被击中的次数为偶数的概率;
(II)若该射手用这3支抢各射击一次,求目标至多被击中一次的概率。