（本小题满分14分） 如图，直角梯形ABCD中，∠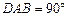
，AD∥BC，AB=2，AD=
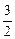，BC=
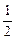,椭圆F以A、B为焦点且过点D. 
（Ⅰ）建立适当的直角坐标系，求椭圆的方程；
（Ⅱ）若点E满足
,是否存在斜率
两点，且
，若存在，求K的取值范围；若不存在，说明理由。
相关试题
在区间[0,
]上的最值
．
时，求
的零点；
有三个不同的实数解，求
的值；
在
上的最小值
.[来
上的函数
是偶函数．
的值；
在
上的单调性，并用定义法证明；
恒成立，求实数
的取值范围推荐套卷
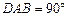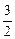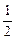（本小题满分14分） 如图，直角梯形ABCD中，∠，AD∥BC，AB=2，AD=，BC=,椭圆F以A、B为焦点且过点D.
（Ⅰ）建立适当的直角坐标系，求椭圆的方程；
（Ⅱ）若点E满足,是否存在斜率两点，且，若存在，求K的取值范围；若不存在，说明理由。
粤公网安备 44130202000953号