（本小题满分10分）选修4—1：几何证明选讲
如图所示，AB是⊙O的直径，G为AB延长线上的一点，GCD是⊙O的割线，过点(
G作AB的垂线，交AC的延长线于点E，交AD的延长线于点F，过G作⊙O的切线，切点为H .求证：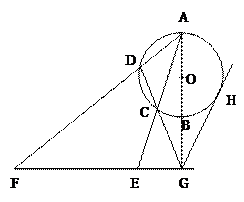
（I）C，D，F，E四点共圆；
（II）GH2=GE·GF.
相关试题
满足：
，其中
为数列
项和.
满足：
，试求
.
的终边分别与单位圆交于
两点．
，点
的横坐标为
，求
的值；
，求函数
的值域．
.
的定义域；
轴；
满足什么关系时，
在
上恒取正值.
是定义在R上的奇函数，当
时，
，其中
且
.
的值；（2）求
（其中
），且
的图像在
轴右侧的第一个最高点的横坐标为
.
的值；（2）如果
在区间
上的最小值为
，求
的值.推荐套卷
（本小题满分10分）选修4—1：几何证明选讲
如图所示，AB是⊙O的直径，G为AB延长线上的一点，GCD是⊙O的割线，过点(
G作AB的垂线，交AC的延长线于点E，交AD的延长线于点F，过G作⊙O的切线，切点为H .求证：
（I）C，D，F，E四点共圆；
（II）GH2=GE·GF.
粤公网安备 44130202000953号