(本小题满分12分)
已知定点A(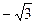
,0),B是圆C:(x-
)2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
(1)求动点E的轨迹方程.
(2)设直线l:y="kx+m" (k≠0,m>0)与E的轨迹交与P,Q两点,且以PQ为对角线的菱形的一顶点为M(-1,0),求△OPQ面积的最大值及此时直线l的方程.
相关试题
，
．证明：当且仅当
时，存在数列
满足以下条件：
，
；
存在；
，
的正整数解组
的个数．
是圆内接四边形．
与
的交点为
，
是弧
上一点，连接
并延长交
于点
，点
分别在
，
的延长线上，满足
，
，求证：
四点共圆． 
求证：
；
在区间（0，2）内至少有一个零点；
是函数
推荐套卷
(本小题满分12分)
已知定点A(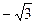,0),B是圆C:(x-)2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
(1)求动点E的轨迹方程.
(2)设直线l:y="kx+m" (k≠0,m>0)与E的轨迹交与P,Q两点,且以PQ为对角线的菱形的一顶点为M(-1,0),求△OPQ面积的最大值及此时直线l的方程.
粤公网安备 44130202000953号