在椭圆 中,
中, 为椭圆上的一点,过坐标原点
为椭圆上的一点,过坐标原点 的直线交椭圆于
的直线交椭圆于 两点,其中
两点,其中 在第一象限,过
在第一象限,过 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接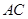 ,
,
(1)若直线 与
与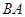 的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;
的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;
(2)若 为
为 的延长线与椭圆的交点,求证:
的延长线与椭圆的交点,求证: .
.
推荐套卷
在椭圆 中,
中, 为椭圆上的一点,过坐标原点
为椭圆上的一点,过坐标原点 的直线交椭圆于
的直线交椭圆于 两点,其中
两点,其中 在第一象限,过
在第一象限,过 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接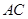 ,
,
(1)若直线 与
与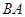 的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;
的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;
(2)若 为
为 的延长线与椭圆的交点,求证:
的延长线与椭圆的交点,求证: .
.