如图①,正三角形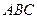 边长2,
边长2,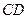 为
为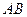 边上的高,
边上的高,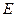 、
、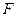 分别为
分别为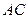 、
、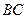 中点,现将
中点,现将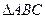 沿
沿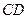 翻折成直二面角
翻折成直二面角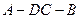 ,如图②
,如图②
(1)判断翻折后直线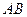 与面
与面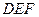 的位置关系,并说明理由
的位置关系,并说明理由
(2)求二面角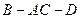 的余弦值
的余弦值
(3)求点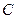 到面
到面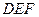 的距离
的距离
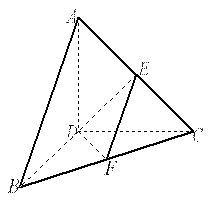
图 ① 图 2
推荐套卷
如图①,正三角形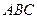 边长2,
边长2,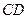 为
为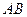 边上的高,
边上的高,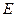 、
、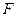 分别为
分别为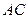 、
、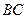 中点,现将
中点,现将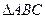 沿
沿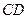 翻折成直二面角
翻折成直二面角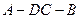 ,如图②
,如图②
(1)判断翻折后直线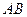 与面
与面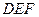 的位置关系,并说明理由
的位置关系,并说明理由
(2)求二面角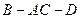 的余弦值
的余弦值
(3)求点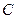 到面
到面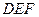 的距离
的距离

图 ① 图 2