已知函数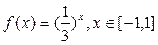 ,函数
,函数
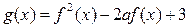 的最小值为
的最小值为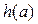 。
。
(1)求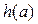 的表达式。
的表达式。
(2)是否存在实数m,n同时满足以下条件:
① m>n>3;
② 当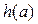 的定义域为[m,n]时,值域为
的定义域为[m,n]时,值域为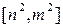
若存在,求出m,n的值;若不存在,说明理由。
相关知识点
推荐套卷
已知函数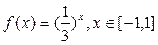 ,函数
,函数
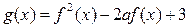 的最小值为
的最小值为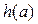 。
。
(1)求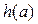 的表达式。
的表达式。
(2)是否存在实数m,n同时满足以下条件:
① m>n>3;
② 当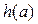 的定义域为[m,n]时,值域为
的定义域为[m,n]时,值域为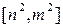
若存在,求出m,n的值;若不存在,说明理由。