(8分)如图,四棱锥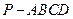 底面是正方形且四个顶点
底面是正方形且四个顶点 在球
在球 的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点
的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点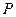 在球面
在球面 上且
上且 面
面 ,且已知
,且已知 。
。
(1)求球 的体积;
的体积;
(2)设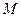 为
为 中点,求异面直线
中点,求异面直线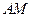 与
与 所成角的余弦值。
所成角的余弦值。

相关知识点
推荐套卷
(8分)如图,四棱锥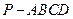 底面是正方形且四个顶点
底面是正方形且四个顶点 在球
在球 的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点
的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点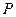 在球面
在球面 上且
上且 面
面 ,且已知
,且已知 。
。
(1)求球 的体积;
的体积;
(2)设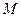 为
为 中点,求异面直线
中点,求异面直线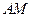 与
与 所成角的余弦值。
所成角的余弦值。
