(本小题满分14分)
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
(Ⅰ) 写出图一表示的市场售价与时间的函数关系式P=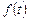 ;
;
写出图二表示的种植成本与时间的函数关系式Q= ;
;
(Ⅱ) 认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/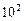 kg,时间单位:天)
kg,时间单位:天)
推荐套卷
(本小题满分14分)
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
(Ⅰ) 写出图一表示的市场售价与时间的函数关系式P=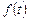 ;
;
写出图二表示的种植成本与时间的函数关系式Q= ;
;
(Ⅱ) 认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/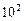 kg,时间单位:天)
kg,时间单位:天)