 个正数排成如下表所示的
个正数排成如下表所示的 行
行 列:
列:
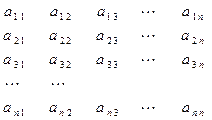
其中每一行成等差数列,每一列成等比数列,且各列的公比相等,若 ,
, ,
,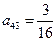 。
。
① 求 ;
;
② 记 ,求
,求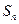 关于
关于 的表达式;
的表达式;
③ 对于②的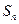 ,求证:
,求证: ;
;
④ 若集合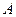 是集合
是集合 的真子集,则称由
的真子集,则称由 的判断到
的判断到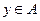 的判断为对
的判断为对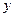 的估计的一次
的估计的一次
优化。请你优化③中的结果。
推荐套卷
 个正数排成如下表所示的
个正数排成如下表所示的 行
行 列:
列:
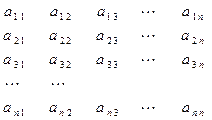
其中每一行成等差数列,每一列成等比数列,且各列的公比相等,若 ,
, ,
,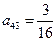 。
。
① 求 ;
;
② 记 ,求
,求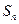 关于
关于 的表达式;
的表达式;
③ 对于②的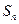 ,求证:
,求证: ;
;
④ 若集合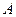 是集合
是集合 的真子集,则称由
的真子集,则称由 的判断到
的判断到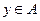 的判断为对
的判断为对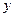 的估计的一次
的估计的一次
优化。请你优化③中的结果。