设直线
. 若直线l与曲线S同时满足下列两个条件：①直线l与曲线S相切且至少有两个切点；②对任意x∈R都有
. 则称直线l为曲线S的“上夹线”．
⑴已知函数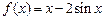
．求证：
为曲线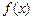
的“上夹线”．
⑵观察下图：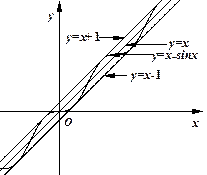
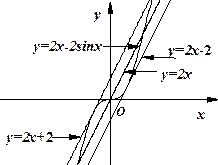
根据上图，试推测曲线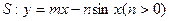
的“上夹线”的方程，并给出证明．
相关试题
,推荐套卷
设直线. 若直线l与曲线S同时满足下列两个条件：①直线l与曲线S相切且至少有两个切点；②对任意x∈R都有. 则称直线l为曲线S的“上夹线”．
⑴已知函数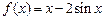．求证：为曲线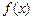的“上夹线”．
⑵观察下图：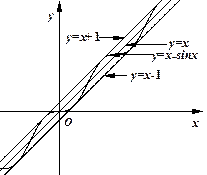
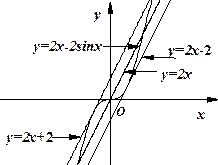
根据上图，试推测曲线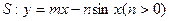的“上夹线”的方程，并给出证明．
粤公网安备 44130202000953号