(本小题满分13分)设数列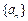 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表:
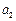
 ……
…… 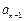
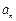 第1行
第1行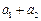
 ……
…… 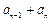 第2行
第2行
… … …
… …
… 第 行
行
上表共有 行,其中第1行的
行,其中第1行的 个数为
个数为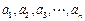 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
.
(1)求证:数列 成等比数列;
成等比数列;
(2)若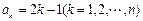 ,求和
,求和 .
.
相关知识点
推荐套卷
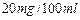 -
-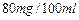 (不含80)之间,属于酒后驾车,血液酒精浓度在
(不含80)之间,属于酒后驾车,血液酒精浓度在 (1)求这40名驾车者中属酒后驾车的人数;(图1中每组包括左端点,不包括右端点)
(1)求这40名驾车者中属酒后驾车的人数;(图1中每组包括左端点,不包括右端点)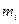 与
与 分别表示图1中各组的组中值及频率)
分别表示图1中各组的组中值及频率) -
-

 中,角
中,角 、
、 、
、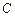 的对边分别为
的对边分别为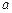 、
、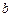 、
、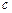 ,且
,且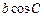 ,
,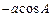 ,
,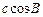 成等差数列.
成等差数列. ,
,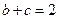 ,求
,求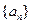 的通项公式是
的通项公式是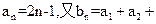 …+
…+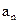
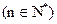
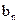 ;
;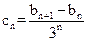 ,求数列
,求数列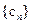 的前n项和.
的前n项和. 中,
中,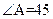 °,BD
°,BD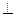 AC,AD=2CD=4,将
AC,AD=2CD=4,将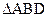 沿BD折起至
沿BD折起至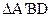 的位置,连结
的位置,连结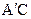 ,(如图2),记二面角
,(如图2),记二面角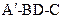 的大小为
的大小为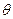 (0<
(0<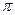 ).
).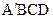 的表面积。
的表面积。 粤公网安备 44130202000953号
粤公网安备 44130202000953号