(本小题满分12分)高二级某次数学测试中,随机从该年级所有学生中抽取了100名同学的数学成绩(满分150分),经统计成绩在 的有6人,在
的有6人,在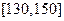 的有4人.在
的有4人.在 ,
, 各区间分布情况如右图所示的频率分布直方图,若直方图中,
各区间分布情况如右图所示的频率分布直方图,若直方图中, 和
和 对应小矩形高度相等,且
对应小矩形高度相等,且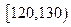 对应小矩形高度又恰为
对应小矩形高度又恰为 对应小矩形高度的一半.
对应小矩形高度的一半.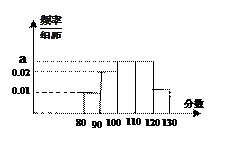
(1)确定图中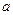 的值;
的值;
(2)设得分在110分以上(含110分)为优秀,则这次测试的优秀率是多少?
(3)某班共有学生50人,若以该次统计结果为依据,现随机从该班学生中抽出3人, 则至少抽到一名数学成绩优秀学生的概率是多少?
推荐套卷
 表示甲胜乙的次数,求
表示甲胜乙的次数,求
 ,其中
,其中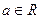 ,若点
,若点 在矩阵
在矩阵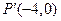 ,
, ,圆
,圆
 为参数).
为参数). ,
, ,
, .
. 时,求
时,求 的单调区间;
的单调区间; 在点
在点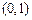 处的切线与直线
处的切线与直线 及曲线
及曲线 ,使
,使 1常数,求函数
1常数,求函数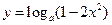 定义
定义 上单调递增;命题Q:不等式
上单调递增;命题Q:不等式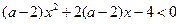 对任意实数
对任意实数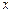 恒成立;若
恒成立;若 是真命题,求实数
是真命题,求实数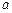 的取值范
的取值范 和外墙需要建造隔热层.
和外墙需要建造隔热层. (单位:cm)满足关系:
(单位:cm)满足关系: ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热
为隔热 的值及
的值及 粤公网安备 44130202000953号
粤公网安备 44130202000953号