给出集合A={-2，-1，
，
，
，1，2，3}
。已知a∈A，使得幂函数
为奇函数，指数函数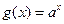
在区间(0，+∞)上为增函数。
（1）试写出所有符合条件的a，说
明理由；
（2）判断f(x)在(0，+∞)的单调性，并证明；
（3）解方程：f[g(x)]=g[f
(x)]。
上点
且与过这点的切线垂直的直线方程．
和曲线
在它们的交点处的两切线的夹角为
，求
的值．
上一点
，用斜率定义求：
，判断
在
处是否可导？
在点
处可导，则函数推荐套卷
给出集合A={-2，-1，，，，1，2，3}。已知a∈A，使得幂函数为奇函数，指数函数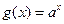在区间(0，+∞)上为增函数。
（1）试写出所有符合条件的a，说明理由；
（2）判断f(x)在(0，+∞)的单调性，并证明；
（3）解方程：f[g(x)]=g[f(x)]。
粤公网安备 44130202000953号