某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为 ,以后每年交纳的数目均比上一年增加 ,因此,历年所交纳的储务金数目 , ,…是一个公差为 的等差数列,与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为 ,那么,在第 年末,第一年所交纳的储备金就变为 ,第二年所交纳的储备金就变为 ,……,以 表示到第 年末所累计的储备金总额.
(Ⅰ)写出
与
的递推关系式;
(Ⅱ)求证:
,其中
是一个等比数列,
是一个等差数列.
相关知识点
推荐套卷
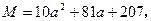
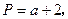
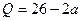 ,若将
,若将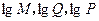
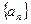 的前三项.
的前三项.
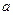 的值及
的值及 )记函数
)记函数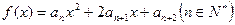 的图象在
的图象在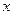 轴上截得的线段长为
轴上截得的线段长为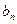 ,设
,设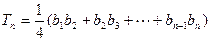 ,求
,求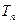
 证明以下命题:
证明以下命题: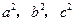 成等差数列。
成等差数列。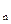 ,其边长
,其边长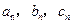 为正整数且
为正整数且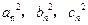 成等差数列。
成等差数列。 中,
中, =0,且对任意k
=0,且对任意k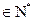 ,
, 成等差数列,
成等差数列,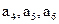 成等比数列;
成等比数列; 的通项公式;
的通项公式; 为等差数列,且
为等差数列,且 ,
,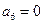 。
。 满足
满足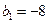 ,
, ,求
,求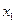 与
与 分别是实系数方程
分别是实系数方程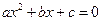 和
和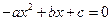 的一个根,且
的一个根,且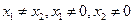 ,求证:方程
,求证:方程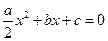 有仅有
有仅有 一根介于
一根介于 粤公网安备 44130202000953号
粤公网安备 44130202000953号