为了了解高中新生的体能情况，某学校抽取部分高一学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中从 左到右各小长方形面积之比为2：4：17：15：9：3，第二小组频数为12﹒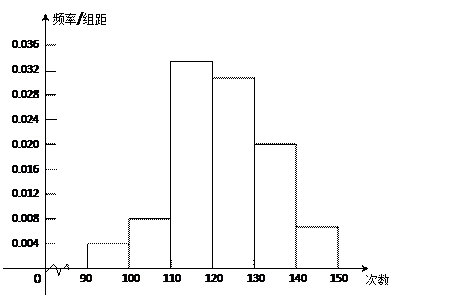
[来
（Ⅰ）第二小组的频率是多少？样本容量是多少？
（Ⅱ）若次数在110以上（含110次）为达标，试估计该学校全体高一学生的达标率是多少？
（Ⅲ）在这次测试中，学生跳绳次数的中位数落在哪个小组内？请说明理由．
相关试题
（本小题满分14分）某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：
| 组号 |
第一组 |
第二组 |
第三组 |
第四组 |
第五组 |
| 分组 |
[50，60） |
[60，70） |
[70，80） |
[80，90） |
[90，100] |
（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；
（3）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？
（本小题满分13分）设关于
的一元二次方程
.
（1）若
是从
、
、
、
四个数中任取的一个数，
是从、、三个数中任取的一个数，求上述方程有实根的概率；
（2）若
是从区间
任取的一个数，
是从区间
任取的一个数，求上述方程有实根的概率.
（本小题满分13分）如图，∠AOB＝60°，OA＝2，OB＝5，在线段OB上任取一点C，试求：
（1）△AOC为钝角三角形的概率；
（2）△AOC为锐角三角形的概率．
（本小题满分13分）据预测，某旅游景区游客人数在
至
人之间，游客人数
（人）与游客的消费总额
（元）之间近似地满足关系：
（1）若该景区游客消费总额不低于
元时，求景区游客人数的范围。
（2）当景区游客的人数为多少人时，游客的人均消费最高？并求游客的人均最高消费额。
（参考公式：当a>0,b>0时，
,当且仅当a=b时等号成立）
，
.若
，求实数
的取值范围.相关知识点
推荐套卷
粤公网安备 44130202000953号