(本小题满分14分)已知函数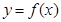 ,
, ,设曲线
,设曲线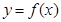 在点
在点 处的切线方程为
处的切线方程为 . 如果对任意的
. 如果对任意的 ,均有:
,均有:
①当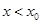 时,
时,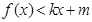 ;
;
②当 时,
时,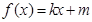 ;
;
③当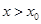 时,
时,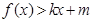 ,
,
则称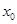 为函数
为函数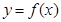 的一个“ʃ-点”.
的一个“ʃ-点”.
(1)判断 是否是下列函数的“ʃ-点”:
是否是下列函数的“ʃ-点”:
① ; ②
; ② .(只需写出结论)
.(只需写出结论)
(2)设函数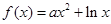 .
.
(ⅰ)若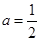 ,证明:
,证明: 是函数
是函数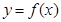 的一个“ʃ-点”;
的一个“ʃ-点”;
(ⅱ)若函数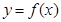 存在“ʃ-点”,直接写出
存在“ʃ-点”,直接写出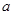 的取值范围.
的取值范围.
相关知识点
推荐套卷
(本小题满分14分)已知函数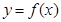 ,
, ,设曲线
,设曲线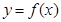 在点
在点 处的切线方程为
处的切线方程为 . 如果对任意的
. 如果对任意的 ,均有:
,均有:
①当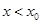 时,
时,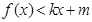 ;
;
②当 时,
时,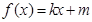 ;
;
③当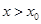 时,
时,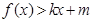 ,
,
则称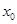 为函数
为函数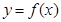 的一个“ʃ-点”.
的一个“ʃ-点”.
(1)判断 是否是下列函数的“ʃ-点”:
是否是下列函数的“ʃ-点”:
① ; ②
; ② .(只需写出结论)
.(只需写出结论)
(2)设函数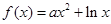 .
.
(ⅰ)若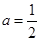 ,证明:
,证明: 是函数
是函数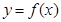 的一个“ʃ-点”;
的一个“ʃ-点”;
(ⅱ)若函数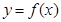 存在“ʃ-点”,直接写出
存在“ʃ-点”,直接写出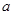 的取值范围.
的取值范围.