已知△ABC是边长为2的正三角形，如图，P,Q依次是AB,AC边上的点，且线段PQ将△ABC分成面积相等的两部分，设AP=x,AQ=t,PQ=y,求：
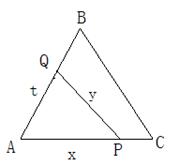
（1）t关于x的函数关系式；
（2）y关于x的函数关系式；
（3）y的最小值和最大值。
相关试题
如图，四棱锥P-ABCD，侧面PAD是边长为2的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．
（1）求证：PC⊥AD；
（2）求点D到平面PAM的距离．
为了调查某高中学生每天的睡眠时间，现随机对20名男生和20名女生进行问卷调查，结果如下：女生：
| 睡眠时间（小时） |
[4,5） |
[5,6） |
[6,7） |
[7,8） |
[8,9] |
| 人数 |
2 |
4 |
8 |
4 |
2 |
男生：
| 睡眠时间（小时） |
[4,5） |
[5,6） |
[6,7） |
[7,8） |
[8,9] |
| 人数 |
1 |
5 |
6 |
5 |
3 |
（1）现把睡眠时间不足5小时的定义为“严重睡眠不足”，从睡眠时间不足6小时的女生中随机抽取3人，求此3人中恰有一人为“严重睡眠不足”的概率；
（2）完成下面2x2列联表，并回答是否有90%的把握认为“睡眠时间与性别有关”？
| 睡眠时间少于7小时 |
睡眠时间不少于7小时 |
合计 |
|
| 男生 |
|||
| 女生 |
|||
| 合计 |
P（ ） |
0．15 |
0．10 |
0．05 |
0．025 |
0．010 |
0．005 |
0．001 |
| k |
2．072 |
2．706 |
3．841 |
5．024 |
6．635 |
7．8879 |
10．828 |
（
，其中n=a+b+c+d）
的前n项和为
，点
均在函数
的图象上；
，求数列
的前n项和
的离心率为
，其左焦点到点
的距离为
.不过原点
的直线
与
相交于
两点，且线段
被直线
平分.
的面积取最大值时直线
的离心率
，过点
，
的直线到原点的距离是
.
的方程；
交双曲线于不同的点
，且
为圆心的圆上，求
的值.相关知识点
推荐套卷
粤公网安备 44130202000953号