本小题满分14分）已知平面区域D由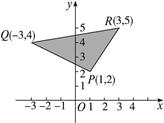
以P（1，2）、R（3，5）、Q（-3，4）为顶点的
三角形内部和边界组成
（1）写出表示区域D的不等式组
（2）设点（x，y）在区域D内变动，求目标函数
Z=2x+y的最小值；
（3）若在区域D内有无穷多个点（x，y）可使目标函数
取得最小值，求m的值。
，设
．
时，求z的取值范围．
（
），且
的最大值为7，求k的值．
．
；
，
，
中至少有一个不小于
．
的最大值．
，
，求证：
．推荐套卷
本小题满分14分）已知平面区域D由
以P（1，2）、R（3，5）、Q（-3，4）为顶点的
三角形内部和边界组成
（1）写出表示区域D的不等式组
（2）设点（x，y）在区域D内变动，求目标函数
Z=2x+y的最小值；
（3）若在区域D内有无穷多个点（x，y）可使目标函数取得最小值，求m的值。
粤公网安备 44130202000953号