(本小题满分12分)
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
求:(Ⅰ)投了2次骰子,棋子才到达顶点B的概率;
(Ⅱ)记投了n次骰子,棋子在顶点B的概率为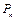 .求
.求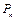 .
.
相关知识点
推荐套卷
(本小题满分12分)
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
求:(Ⅰ)投了2次骰子,棋子才到达顶点B的概率;
(Ⅱ)记投了n次骰子,棋子在顶点B的概率为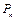 .求
.求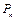 .
.