甲、乙两人在罚球线投球命中的概率分别为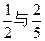
，且各次投球相互之间没有影响．
（1）甲、乙两人在罚球线各投球一次，求这二次投球中恰好命中一次的概率；
（2）甲、乙两人在罚球线各投球二次，求这四次投球中至少有一次命中的概率．
满足
，且有
时，求证：
的不等式
的解集不是空集，求参数
的取值范围。
相关知识点
推荐套卷
甲、乙两人在罚球线投球命中的概率分别为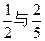，且各次投球相互之间没有影响．
（1）甲、乙两人在罚球线各投球一次，求这二次投球中恰好命中一次的概率；
（2）甲、乙两人在罚球线各投球二次，求这四次投球中至少有一次命中的概率．
粤公网安备 44130202000953号