(本题满分12分)．已知三棱锥P—ABC中，PC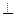
底面ABC，AB=BC，D、F分别为
AC、PC的中点，DE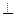AP于E。
（1）求证：AP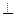平面BDE；
（2）若AE：EP=1：2，求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
 |
，求f（
）的值.
－α）=－cosα；
，cos（α+β）=1，求证：cos（2α+β）=
．推荐套卷
(本题满分12分)．已知三棱锥P—ABC中，PC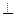底面ABC，AB=BC，D、F分别为
AC、PC的中点，D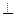EAP于E。
（1）求证：AP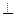平面BDE；
（2）若AE：EP=1：2，求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
|
粤公网安备 44130202000953号