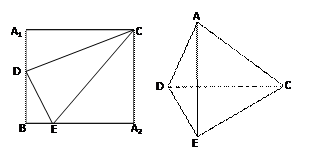
（本小题满分12分）如图，正方形A1BA2C的边长为4，D是A1B的中点，E是BA2上的点，将△A1DC及△A2EC分别沿DC和EC折起，使A1、A2重合于A，且二面角A－DC－E为直二面角。
（1）求证：CD⊥DE； （2）求AE与面DEC所成角的正弦.
 |
相关试题
上的函数
，对任意的
有
，且
．
的值； 
，使
，试问
中，
，
，
．
；
，
，求三棱柱
和矩形
所在的平面互相垂直，
，
，
是线段
的中点．
的体积；
//平面
;
＝
，
＝
，试用
。
中，
底面
，
，点
在线段
上，且
平面
;
，
，
，
，求四棱锥推荐套卷
（本小题满分12分）如图，正方形A1BA2C的边长为4，D是A1B的中点，E是BA2上的点，将△A1DC及△A2EC分别沿DC和EC折起，使A1、A2重合于A，且二面角A－DC－E为直二面角。
（1）求证：CD⊥DE； （2）求AE与面DEC所成角的正弦.
|
粤公网安备 44130202000953号