(本小题满分12分)上海世博会举办时间为2010年5月1日~10月31日。福建馆以“海西”为参博核心元素,主题为“潮涌海西,魅力福建”。福建馆招募了60名志愿者,某高校有l3人入选,其中5人为中英文讲解员,8人为迎宾礼仪,它们来自该校的5所所学院(这5所学院编号为1~5号),人员分布如图所示。若从这13名入选者中随机抽取3人。
(1)求这3人所在学院的编号恰好成等比数列的概率;
(2)求这3人中中英文讲解员人数的分布列及数学期望。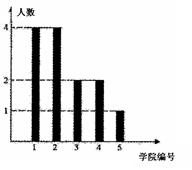
相关知识点
推荐套卷
 关于直线
关于直线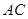 对称,
对称,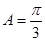 ,
,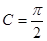 ,
, .把
.把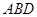 沿
沿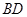 折起(如图2),使二面角
折起(如图2),使二面角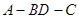 的余弦值等于
的余弦值等于 .
.
 两点间的距离;
两点间的距离;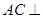 平面
平面 ;
;
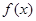 的解析式;
的解析式; 轴的正半轴及
轴的正半轴及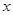 轴的正半轴三者围成图形的面积。
轴的正半轴三者围成图形的面积。 中,
中,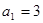 ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且 ,
, 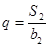 .
.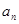 与
与 ;
; .
.
 且
且 ,求
,求 的最小值.
的最小值. ,1),倾斜角
,1),倾斜角 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为 。
。 粤公网安备 44130202000953号
粤公网安备 44130202000953号