(本小题14分) 已知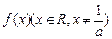 满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使
满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使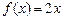 成立的实数x有且只有一个.
成立的实数x有且只有一个.
(1)求 的表达式;
的表达式;
(2)数列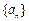 满足:
满足: , 证明:
, 证明: 为等比数列.
为等比数列.
(3)在(2)的条件下, 若 , 求证:
, 求证:
推荐套卷
(本小题14分) 已知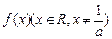 满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使
满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使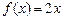 成立的实数x有且只有一个.
成立的实数x有且只有一个.
(1)求 的表达式;
的表达式;
(2)数列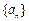 满足:
满足: , 证明:
, 证明: 为等比数列.
为等比数列.
(3)在(2)的条件下, 若 , 求证:
, 求证: