17． (本小题满分13分)
某工厂在试验阶段大量生产一种零件．这种零件有
、
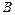两项技术指标需要检测，设各项技术指标达标与否互不影响．若有且仅有一项技术指标达标的概率为
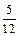，至少一项技术指标达标的概率为
．按质量检验规定：两项技术指标都达标的零件为合格品．
(1) 求一个零件经过检测为合格品的概率是多少？
(2) 任意依次抽出5个零件进行检测，求其中至多3个零件是合格品的概率是多少？
(a＞0,a≠1)
若q是p的必要不充分条件，求实数
的取值范围。
满足条件
，及
.
上的最值.
（
），试问m为何值时， 
为实数？ 
推荐套卷
17． (本小题满分13分)
某工厂在试验阶段大量生产一种零件．这种零件有、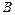两项技术指标需要检测，设各项技术指标达标与否互不影响．若有且仅有一项技术指标达标的概率为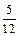，至少一项技术指标达标的概率为．按质量检验规定：两项技术指标都达标的零件为合格品．
(1) 求一个零件经过检测为合格品的概率是多少？
(2) 任意依次抽出5个零件进行检测，求其中至多3个零件是合格品的概率是多少？
粤公网安备 44130202000953号