甲、乙、丙三人组成一组，参加一个闯关游戏团体赛，三人各自独立闯关，其中甲闯关成功的概率为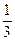
，甲、乙都闯关成功的概率为
，乙、丙都闯关成功的概率为
，每人闯关成功得2分，三人得分之和记为小组团体总分.
（1）求乙、丙各自闯关成功的概率；
（2）求团体总分为4分的概率；
（3）若团体总分不小于4分，则小组可参加复赛，求该小组参加复赛的概率.
相关试题
的图
象.
时函数的值域
，求
的值：
。
m恒成立，求m的最大值；
ax
+blnx在x=1处有极值
.
。
的最小正周期T，并求出函数
]内使推荐套卷
甲、乙、丙三人组成一组，参加一个闯关游戏团体赛，三人各自独立闯关，其中甲闯关成功的概率为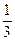，甲、乙都闯关成功的概率为，乙、丙都闯关成功的概率为，每人闯关成功得2分，三人得分之和记为小组团体总分.
（1）求乙、丙各自闯关成功的概率；
（2）求团体总分为4分的概率；
（3）若团体总分不小于4分，则小组可参加复赛，求该小组参加复赛的概率.
粤公网安备 44130202000953号