已知以原点
为中心，
为右焦点的双曲线
的离心率
.
（Ⅰ）求双曲线
的标准方程及其渐近线方程；
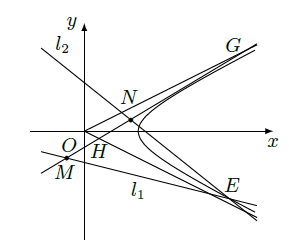
（Ⅱ）如题图，已知过点
的直线
与过点
（其中
）的直线
：
的交点
在双曲线
上，直线
与双曲线的两条渐近线分别交于
、
两点，求
的值.
相关试题
是R上的单调函数，且"x∈R，
，若
，其中m∈R且m > 0
且a≠1，数列
中，
，
(
)，令
，求数列
的前n项和Sn；
，
，n∈N*，求a的取值范围
，
(ω>0)，函数
的最小正周期为π
的单调递减区间及对称中心；
上的最大值与最小值．
，
，a∈R，若“x∈A”是“x∈B”的必要条件，求a的取值范围
中，
，
，
的前20项的和．相关知识点
推荐套卷
已知以原点
为中心，
为右焦点的双曲线
的离心率
.
（Ⅰ）求双曲线
的标准方程及其渐近线方程；
（Ⅱ）如题图，已知过点
的直线
与过点
（其中
）的直线
：
的交点
在双曲线
上，直线
与双曲线的两条渐近线分别交于
、
两点，求
的值.
粤公网安备 44130202000953号